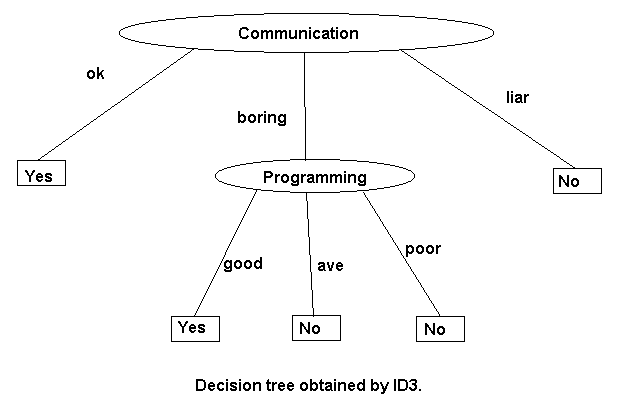
Decision Tree when Prog. is chosen as root. Alternatively we can construct the following decision tree taking ("Pres.") as root.
The time spent in obtaining knowledge from human experts can greatly increase the cost of developing an expert system. One approach that is often used is to learn a decision tree from a table of examples. This approach is based on Quinlan's Algorithm known as ID3.
Ref. J.R.Quinlan, Discovering rules by induction from large collection of examples ,in D. Michie(ed.), Expert Systems in the Microelectronic Age, 168-201, Edinburgh Univ.Press,1979.
ID3 takes a table of examples as input and produces a decision tree a table of examples. We shall describe ID3 with the aid of the following example.
Example:
A recruitment agency which specialises
in recruiting trainee programmers wants to develop a decision tree to filter
out unsuitable applicants.
The agency we three criteria to
make this decision: programming ability(Prog.), communication ability*Com.)
& presentation(Pres.).
Suppose the Agency provide the examples
in the following Table:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1- Choose an attribute as the root. Only those attributes that are not ancestors are eligible. Initially, all the attributes except the "Decision" attribute are eligible.
2- Create an arc for each possible value of the root. Label the arcs with their value.
3- Partition the table into sub-tables; one for each arc. A sub table for a particular arc must have exactly those examples of the table whose root has the value, labelling the arc.
4- Repeat the process on those sub-tables whose "Decision" attribute
has different values.

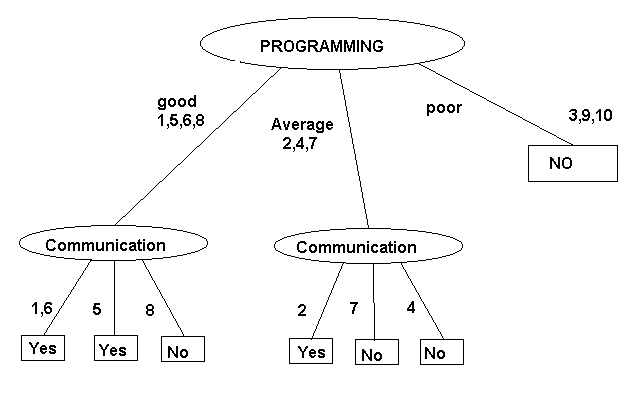
Decision Tree when Prog. is chosen as root. Alternatively we can construct
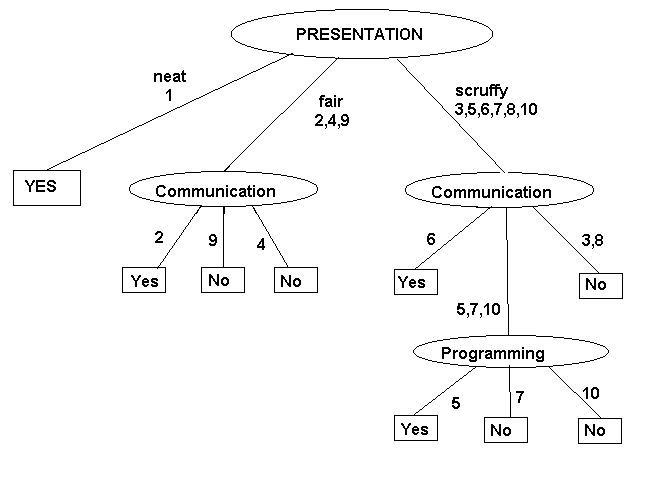
the following decision tree taking ("Pres.") as root.

Above figures show two different decision trees that result
when different attributes are chosen as the root. Notice that although
both these trees are consistent with the examples, they are not equivalent.
Thus, for example, a candidate who is neat
but a liar and a poor
programmer is accepted by the second tree. However, the candidate
would rightly be rejected by the first tree.
This problem occurs in the second tree because we choose
an attribute which does not give much information
about the final classification.
So the question is "How can we choose an attribute which
will result in a good tree?"
- We should choose an attribute which gives the most information.
- Information Theory provides a suitable measure.
![]()
Information cannot be measured by the extent to which it clarifies the unknown. If told something known, there is no or less information.
AV. information/message is called entropy(H).
H is a measure of the amount of info. in a message that
is based on the log of the no. of equivalent messages.

For a discrete probability distribution(yes/no). (H is
also measurement of uncertainty of var X for eg., H(X)).
For example, how much info. would we gain by knowing whether
the decision is a yes or a no if we already know how good the candidate
is at programming.
Conditional entropy or equivocation H(C/A) is a measure
of reduction of uncertainty about decision C given the possible attributes(A).
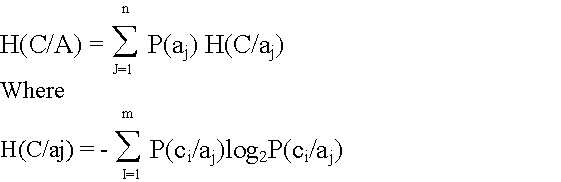
Where "aj" are the "n" values of the attribute A, and the "ci" are the "m" values of the decision c.
For example, we can calculate H(Decision/Prog) by first
using the letter formula to obtain H(Decision/aj) for each of programming
ability.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
and then use the former formula to obtain:
![]()
Similarly we obtain;
H(Decision/Comm) = 0.325
H(Decision/Pres) = 0.827
Thus we know "comm. ability " will give us the least uncertainty
about final decision.
We now partition the examples into tables.
TABLE-1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TABLE-2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TABLE-3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|