[
ARTIFICIAL INTELLIGENCE (C.ENG 303)
]
![]()
Game playing demonstrates several aspects of intelligence,particularly ability to plan (at both immmediate tactical-level and long-term strategic level) and the ability to learn.
Successful game playing is generally deemed to require intelligence. Computers can be programmed to play games such as tic-tac-toe, chequers, chess, etc.
State-of-the-art;
Algorithms run on contemporary computers are achieving "grand master" status in chess.
One-player games , ("You againts the problem" games.E.g Rubik's cube, jig-saw puzzle )
In this course we will study two person, (Here, moves are constrained by the fact that one's opponent will exploit any opportunities which you make available)
Perfect information, (At any given time during the game both players know everything there is to know about the opponent's position. Card games in which you don't know what cards your opponent holds are not perfect information games).
Zero-sum, (if one side wins, then the other loses. e.g. "war- games" are a class of non-zero-sum games), GAMES.
![]()
We can represent all possible games(of a given type) by a directed graph often called a game tree.
The nodes of the graph represent the states of the game. The arcs of the graph represent possible moves by the players (+ and -).Consider the start of a game
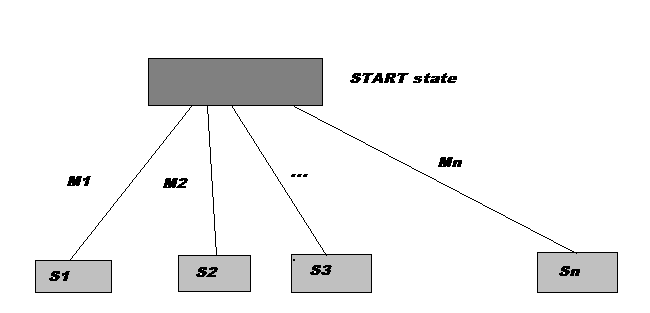
The game starts in some "start" state, and there is a set of possible moves: m1, m2.. mN. These give rise, respectively, to states: S1, S2.. SN.
By considering possible moves at any state Si (recursively), we develop a "game tree".
The leaves of this tree ("tip nodes") represent the state of play so far.
The rules of the game assign a value to every terminal position.
W -- Won
L -- Lost From the point of view of '+'
D -- Drawn
One way to guarantee a good game would be to analyse completely the game tree. However, for a moderate game tree containing about 1040 nodes, if we make an optimistic assumption that 3 nodes can be considered per nanosecond, then it would take 1021 centuries to explore the whole tree. Clearly this is out of question regardless of which search technique we use.
The mini-max rule of classical game theory due to Von Neumann, allows terminal values to be "backed up" the game tree, and hence defines an optimal strategy.
Having fixed scores for the terminal positions how do we analyse the tree? Let us consider the following subtree
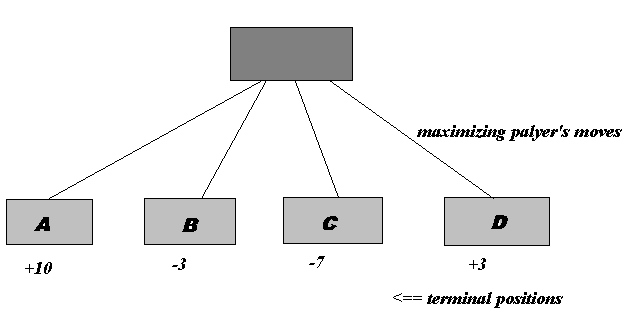
Clearly, the maximising player will choose move A. Conversely, had it been the turn of the minimising player, s/he would choose move C.
If we look further ahead, the game tree may look like this:
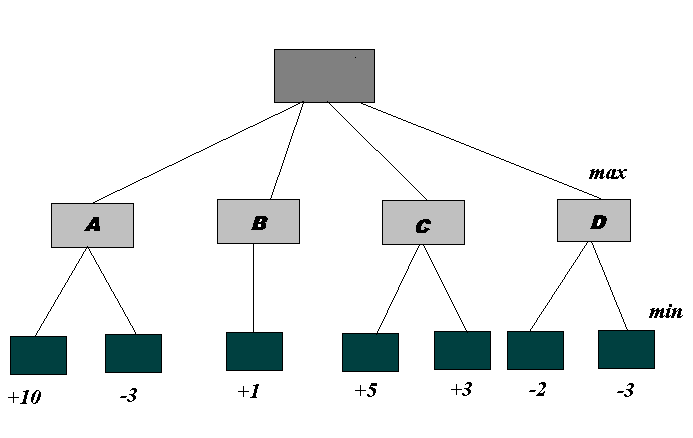
Is A the best move? No, because the minimising player can be assumed to take the - 3 branch to maximise his/her chances; so move B, for instance, would be better. In fact, C is best, because the minimising can only take the +3 branch at best.
Can we formalise this procedure?
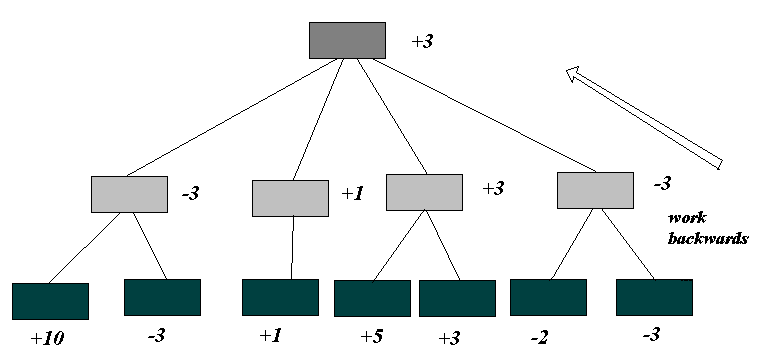
Starting with the scores of the terminal positions we work backwards up the game tree, labelling the nodes as indicated above. If the minimising player has the choice of move we label the node with the lowest possible score from the available alternatives.If the maximising has the choice, we label the node with the highest possible score. This process can be carried to any depth, so, using this mini-max rule a value can be assigned to every node. In particular, a value can be assigned to the initial node (this is + 3 in the example above). This value is known as the value of the game.
Starting from any node, a rational (i.e. faultless) player executes only value-preserving moves.
Let us take a look at some practical considerations: How big are typical game trees? Construction of a complete game tree is feasible only for simple games
Example 1 - Tic -Tac - Toe
First consider the game tree.
An upper bound
1st move 9 pass
2nd move 8 pass
9th move 1 pass
A total of 362,880 terminal positions.The game tree for checkers(draughts) has about 1040 nodes.
Alternatively,
There are 9 positions, each occupied by a "O", "X" or null.
39 = 19, 683 positions in all. Question: How do you reconcile these two estimates?
Example 2 - Chess
The average "branching factor" is probably about 35. Typically each player makes 50 moves. Thus size of the game tree is
35100 = 10 150 E.g. 1 node exploration pico second & 3 x 107 secs/year.
Therefore, 10 130 years. Branching Factor - Average number of legal moves possible at a given position in a game
Games for which a complete tree can be feasibly constructed are not very interesting , since the best course of play can be computed at the start.
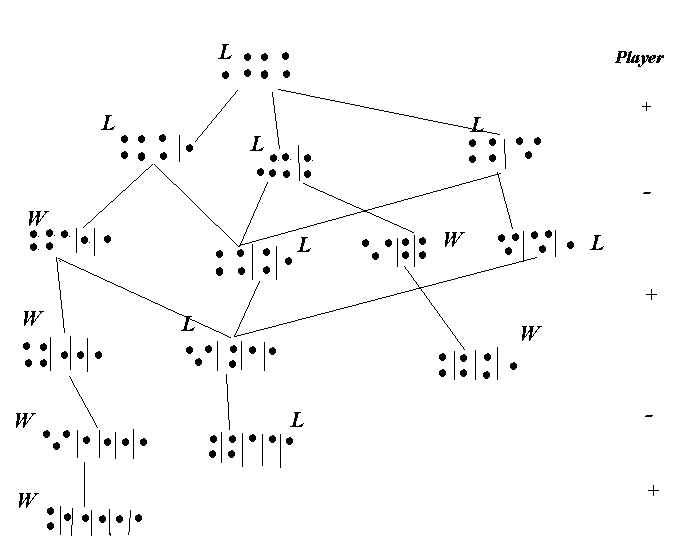
A heap of 7 objects is given. Each player alternately tries to divide any one of the heaps into two unequal ones. Loser is one who cannot play.
Exercise Start off with 7 objects and draw the "game-tree" for Grundy's game. Then mark in values of terminal nodes and back these up.
Solution:
4.4 Static Evaluation Function
This is used to evaluate positions at the leaves of the tree.
For non-trivial games, it is not practicable to mini-max on the entire game tree. Reasonable results may be obtained however, by:
- growing as big a game tree as practicable and then
- using a "static evaluation function" to assign approximation values to nodes on the "horizon" and then
- mini-maxing from there.
Example Consider the game tic-tac-toe. Assume that "+" plays X and "-" plays 0. A plausible static evaluation function is score +1 for each row, column or diagonal still open for (+). And -1 for each row, column or diagonal still open for (-).
E.g.
YOU CAN PLAY TIC-TAC-TOE GAME HERE
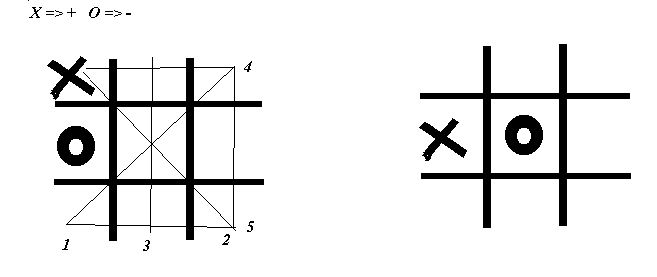
|
6-5 = +1 |
4 -6 = -2 |
| (advantage for +) |
(Big advantage to - ) |
An evaluation function is specific to the game being played. A static evaluation function is not perfect! If it was then the mini-max technique would be redundant, and ideal(i.e. value preserving) play would be possible.
A typical SEF for chess might comprise
This method is a refinement of the mini-max technique. The mini-max technique involved inspecting all nodes down to some depth N, as follows:
- Evaluate all terminal nodes
- Assign backed up values, starting at level N-1 and working up to level 1.
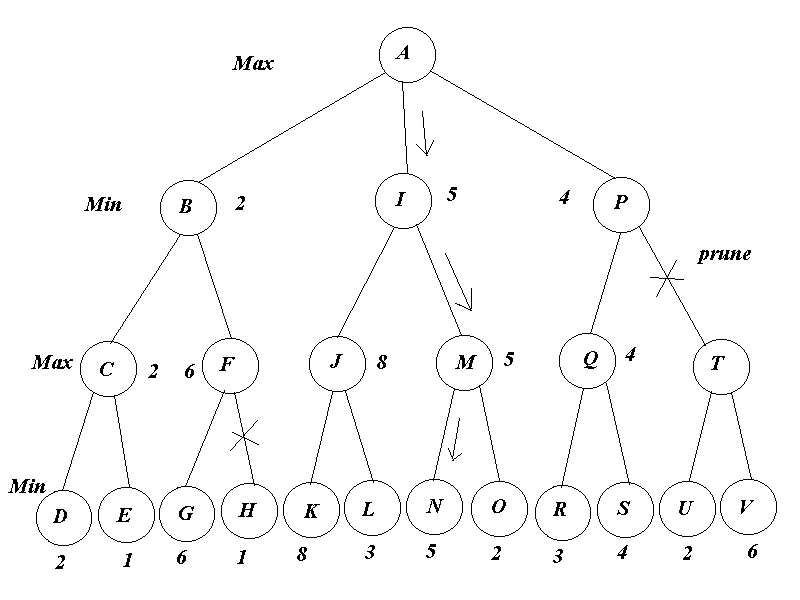
Alpha-beta pruning follows much the same lines except that certain sub-trees can be rejected ("pruned") as they are encountered, considerably reducing the search effort.
Essentially, we keep track of the "best move so far" available to each player, and reject any subtrees which can only produce a worse result.
Consider a situation in which the MIN- children of a MAX-node have been partially inspected.
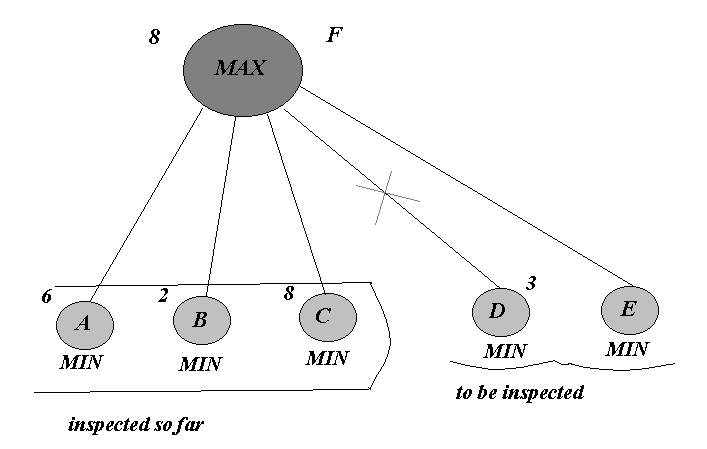
At this point the "tentative" (backed up»so far) value of F is 8.
MAX is not interested in any move which offers a value of less than 8, since it is already known that 8 is the worst that MAX can do, so far
Thus the node D and all its descendents, can be pruned, since MIN will certainly opt for a value of 3 rather than 8.
(In a similar fashion, node B would have been pruned earlier in the process). Similarly for a MIN-node:
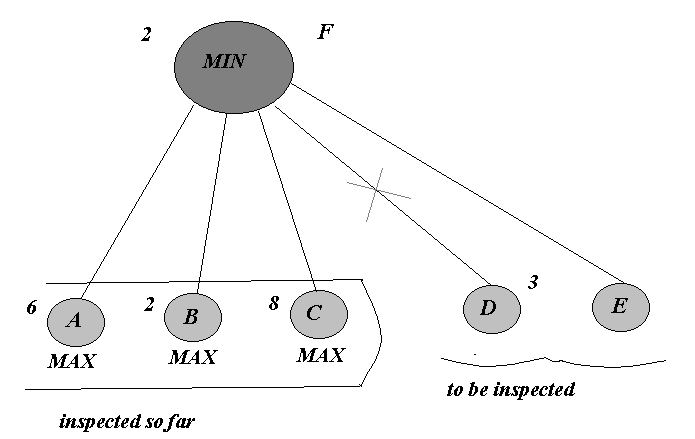
MIN is trying to minimise the game-value. So far, the value 2 in the best available from MIN's point of view. MIN will immediately reject node D, which can be pruned (One can imagine MAX and MIN both watching over the search as it proceeds, keeping track of their best option so far, and rejecting anything which is "worse" from their point of view)
Example (Alpha-Beta Pruning)
| This page is maintained by: | Mehmet R.TOLUN tolun@ceng.metu.edu.tr |
| Last updated at: |